AlterMedicine

Эта математическая последовательность образуется, когда, начиная с единицы, каждое последующее число возникает из суммы двух предыдущих. Вторая единица получается сложением 1 + 0 = 1. Двойка – это 1 + 1 = 2, тройка – это 2 + 1 = 3 и т. д.

Данный числовой ряд всегда приближается к некоторому постоянному соотношению. Если какой-либо член последовательности Фибоначчи разделить на предшествующий ему (например, 13: 8), то в результате получается величина, колеблющаяся около значения 1,61803398875… Однако это соотношение иррационально, то есть представляет собой число с бесконечной, непредсказуемой последовательностью десятичных цифр в дробной части. Его невозможно выразить точно. Деление других членов последовательности дает число, близкое к этому значению, но не равное ему. Принято считать это соотношение условно равным 1,618. В алгебре его обозначают греческой буквой φ (фи). Если, наоборот, какой-либо очередной член последовательности разделить на последующий (например, 8: 13 или 13: 21 и т. д.), то получится величина, стремящаяся к числу 0,618, которое в свою очередь равно числу, обратному числу «фи», то есть 1: 1,618. При росте порядкового номера члена числового ряда эти соотношения стремятся к иррациональным числам, равным (5–1): 2 и (5 + 1): 2 соответственно. Особые названия этому соотношению начали давать еще до того, как средневековый математик Лука Пачиоли назвал его божественной пропорцией. Среди современных названий есть такие, как золотое сечение, золотое среднее и отношение вертящихся квадратов. Астроном Кеплер называл это соотношение одним из сокровищ геометрии.

Приступим к практическому применению золотого сечения для строительства небольшой пирамиды. Чертеж развертки пирамиды имеет следующий вид.

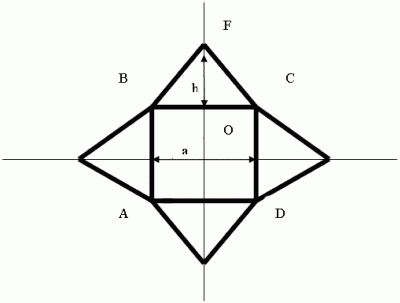
Рис. 7. Развертка пирамиды.

Обозначим:

а) длину основания пирамиды буквой а = |AB| = |BC|;

б) высоту боковой грани пирамиды буквой h = |OF|;

в) высоту самой пирамиды буквой H;

г) тогда h = φn x a, где φ1 = 1,618 или φ2 = 0,618; так как φ может принимать два значения, то для построения возможны две пирамиды:

1) высотная пирамида (ее пропорции использовали, например, при строительстве сталинских высоток в Москве);

2) приземленная пирамида (таковы египетская, мексиканская, перуанская, бермудская пирамиды).

Высотная пирамида обладает способностью увеличивать энергию находящихся внутри нее объектов. Она поднимает энергетический ресурс человека и общий потенциал биополя.

Приземленная пирамида хорошо уравновешивает энергию и заделывает энергетические пробои (порчу, сглаз, проклятие).

Рассмотрим образец расчета каждой из этих пирамид. Для упрощения возьмем длину основания, равную 1 дм = 10 см.

1) Высотная пирамида: h = φ1 x a = 1,618 x 10 = 16,18 см.

2) Приземленная пирамида: h = φ2 x a = 0,618 x 10 = 6,18 см.

Начертите развертку пирамиды, допустим, на картоне в соответствии с полученными размерами и сложите ее, закрепляя грани между собой, например скотчем. Таким образом ваша первая миниатюрная пирамида станет настольной. Ее можно использовать для обработки семян, которые вы собираетесь высевать на участке. Но самое главное, что ее можно устанавливать основанием на больную область вашего тела. Понятно, энергетика такой пирамиды ввиду ее малого размера требует продолжительного воздействия. Ведь чем меньше пирамида, тем слабее ее мощность, точнее, мощность проходящего через нее излучения геомагнитного поля. Наша модель – это, так сказать, комнатный вариант.